Multiscale Homogenization of Viscoelastic Unidirectional Composites

Researchers

Description

This work focuses on the derivation of effective properties for composite laminates consisting of unidirectional carbon fibers in an epoxy resin. The major goal is to provide efficient tools, capable of representing the overall effective mechanical and thermal behavior by considering the viscoelasticity of the epoxy resin and the micro scale geometry of the composite.

The process of determining effective properties representing the macroscopic behavior of a heterogenous material is called homogenization. The most intuitive approach is the homogenization method referred to as Variational Bounds. The homogenization is then achieved by basically imposing a certain strain field onto the heterogenous micro structure and comparing it to the homogeneous case by equating the strain or complementary energy. Depending on which energy has been chosen for the equivalence, either a upper or a lower bound will be computed (Reuss-Voigt bounds). In this straightforward approach the modeling and simulation of the composites micro structure is done by the use of commercial finite element software, eg. Abaqus. The following figure depicts a unit cell onto which the strain field for the load case corresponding to the mechanical properties in the x direction.

This approach has the advantages of being intuitive, physically based and the fact that commercial software can be used for all simulations. But unfortunately, there are several drawbacks. For instance, the results provided by this method are bounds, and hence do not converge towards the exact effective properties. Moreover, a laborious post-processing is necessary to complete the homogenization (superposition of load cases, computing and computing the energies, curve fitting to prony series). Further disadvantages are, this method is time consuming in the case of viscoelasticity (solve problem over several decades of time), inaccuracies due to curve fitting of results etc. A promising candidate to provide an accurate and efficient approach is the so called Asymptotic Expansion Homogenization. This method expands the displacement field into a series of finite terms by assuming scale separation (micro/macro scale) and periodicity of the microstructure.

For time-dependent homogenization, asymptotic Expansion Homogenization is more efficient since it utilizes the fact that the viscoelasticity is expressed by a Prony series which can transformed into the Laplace space. Additionally, Asymptotic Expansion Homogenization is capable of homogenizing any material property without the need of setting up a new scheme. It also provides an approximation of the exact effective properties instead of bounds. Last but not least, it is one of the few homogenization methods for which a convergence towards the effective material properties can be prooved. This is why, a good agreement with experiments can be achieved. But, implementing this method brings up a major problem; there is no commercial software for this homogenization. Consequently, one has to write one's own finite element code. In addition, writing and changing this code involves background knowledge of homogenization theory.

The properties obtained by this homogenization technique have been compared to several creep experiments, including tension, shear and four point bending test.

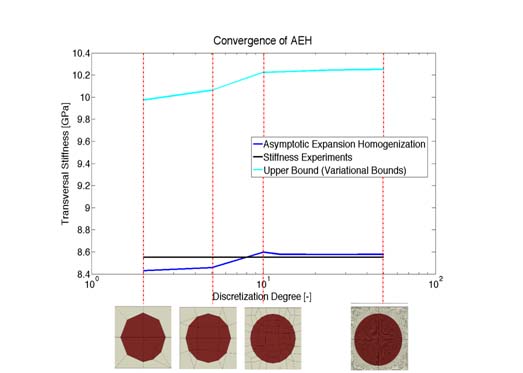
The following figure shows the mesh sensitivity of both methods. It also provides a comparison with an short time tensile test.